Map and explore the temperature measurements
First, you will download the temperature measurements and add them to a map. Then, you will explore the data with a histogram to confirm that an urban heat island effect is present.
Download and explore the project
You will download the project containing the temperature measurements and open it in ArcGIS Pro.
- Download the Analyze_Urban_Heat_Using_Kriging.zip file.
- Locate the downloaded file on your computer.
Note:
Depending on your web browser, you may have been prompted to choose the file's location before you began the download. Most browsers download to your computer's Downloads folder by default.
- Right-click the file and extract the contents to a convenient location on your computer, such as your Documents folder.
- Open the unzipped folder to view the contents.
- If you have ArcGIS Pro installed on your computer, double-click Analyze_Urban_Heat_Using_Kriging.ppkx and open the project. Sign in with your ArcGIS Account.
Note:
If you don't have access to ArcGIS Pro or an ArcGIS organizational account, see options for software access.
The project opens in ArcGIS Pro.

The Madison Temperature map consists of the World Light Gray Canvas Base basemap and two feature layers: Temperature_Aug08_8pm and Block_Groups. The Temperature_Aug08_8pm layer contains 139 points spread across Madison, Wisconsin, covering the city center and surrounding rural areas. Each point represents the location of a sensor measuring temperature at 15-minute intervals. The points in the Temperature_Aug08_8pm layer represent temperature measurements in degrees Fahrenheit taken on August 8, 2016, at 8:00 p.m. at each of the sensors.

In the layer, sensor locations are symbolized in shades of yellow to red representing temperature in degrees Fahrenheit. The lightest shade of yellow corresponds to 73 degrees Fahrenheit (22.78 degrees Celsius), and the darkest shade of red corresponds to 86 degrees Fahrenheit (30 degrees Celsius).
- On the ribbon, on the Map tab, in the Navigate group, click Explore.
- Pan and zoom around the city of Madison to get a sense of the area and the location of sensors.
Note:
A city center can be over 10 degrees warmer than the surrounding countryside. In Madison, higher temperatures are found in the middle of the city, and lower temperatures in the surrounding suburban and rural areas. This suggests the presence of the urban heat island effect, but more quantitative analysis is needed to confirm the effect.
- In the Contents pane, right-click Temperature_Aug08_8pm, and choose Attribute Table to open the attribute table for this layer.

The attribute table for Temperature_Aug_08_8pm appears. The table contains a record of attribute values for each of the 139 individual sensor points. The TemperatureF field maintains the temperature measurement value.
- In the Temperature_Aug08_8pm table, right-click the TemperatureF field and choose Sort Descending.
In the TemperatureF field, the highest temperature recorded is 83.869 degrees Fahrenheit and the lowest recorded value is 73.429.
- Close the Temperature_Aug08_8pm table.
- On the map, zoom to the red sensors in the city center, between Lake Mendota and Lake Monona.

Note:
Many of the highest temperature locations found within the city center are also in close proximity to lakes. The lakes may be contributing to higher temperatures in the summer (August) by increasing humidity levels in the surrounding areas. For this study, you will ignore this factor, but it may warrant additional exploration later as you refine your workflow.
- In the Contents pane, turn on the Block_Groups layer.

The Block_Groups layer represents census block groups in the city of Madison and surrounding townships. Block groups are symbolized by the density of residents over the age of 65, calculated by dividing the population over age 65 by the area of the block group in square kilometers.
- Right-click Block_Groups and choose Zoom To Layer.
These block groups will serve as the extent of the study area for the exercise.

- In the Contents pane, uncheck Block_Groups.
Next, you will predict the average temperature in each block group to locate areas of Madison that are characterized by both high average temperatures and a high density of residents over the age of 65.
Create a histogram chart for temperature
The first step in developing an interpolation workflow for temperature in Madison is to explore the data and look for interesting features. You can gain a lot of insight by looking at the symbolized points on the map, but you should also explore the data using interactive charts. For this data, a histogram chart is most relevant. The histogram chart allows you to see the distribution of temperature values. You will explore the chart to find the areas with the highest and lowest temperature measurements on the map.
- In the Contents pane, right-click Temperature_Aug08_8pm, point to Create Chart, and choose Histogram.

The Chart Properties panes and a chart view appear. Initially, the chart view is empty.
- In the Chart Properties pane, on the Data tab, under Variable, for Number, choose TemperatureF.
The chart updates to show a histogram of temperature measurements and the chart title Distribution of TemperatureF appears. Additionally, the Statistics group in Chart Properties updates, showing various statistics for the TemperatureF histogram field.
- In the Statistics group, leave Mean checked, and check Median and Std. Dev.

In the chart, a blue vertical line is displayed at the mean (average) temperature value (79.4 degrees). Temperature values are spread fairly evenly between the minimum and the maximum, with the largest number of points showing a temperature between 79.5 and 81.3 degrees. The median temperature is displayed in purple and the standard deviation in brown.

In the Chart Properties pane, under Statistics, the Count value is 139 points and the Min and Max temperature values are 73.4 and 83.9 degrees, respectively.
- In the Distribution of TemperatureF histogram, drag a box over the left two bins to select all points that represent locations with the lowest temperature measurements.

The points with the lowest temperature measurements are selected on the Madison Temperature map. These lower temperature measurements are located mostly in the suburban and rural areas surrounding the Madison city center.

- In the Distribution of TemperatureF histogram, drag a box over the last two bins on the right to select locations with the highest temperature measurements.

In the Madison Temperature map, most of the highest temperature measurements are located in the downtown city center area of Madison and in adjacent areas to the northeast and southeast of the city center.
- Close the Chart Properties pane and Chart view.
- On the ribbon, on the Map tab, in the Selection group, click Clear to unselect features.

- In the Quick Access Toolbar, click the Save button to save your Madison Temperature project.

Note:
A message may appear warning you that saving this project file with the current ArcGIS Pro version will prevent you from opening it again in an earlier version. If you see this message, click Yes to proceed.
In the Madison Temperature map, most of the highest temperature measurements are located in the downtown city center and to it northeast and southeast.
You used a histogram to explore distribution of temperature measurements. You found that higher temperature measurements were situated in and around the city center, and that lower temperature measurements were observed in the surrounding suburban and rural areas. This distribution of the temperature values strongly suggests the presence of the urban heat island effect. Next, you will use the Geostatistical Wizard to interpolate temperature measurements to create a temperature map for the entire city of Madison and surrounding townships.
Interpolate temperature using simple kriging
Previously, you mapped and explored the distribution of temperature measurements in Madison, Wisconsin, on August 8, 2016, at 8:00 p.m. By looking at the points symbolized with a graduated yellow-to-red color range and using selections in the histogram chart, you found strong visual evidence of the urban heat island effect at that date and time. Next, you will use the Geostatistical Wizard to interpolate the point temperature measurements and create a continuous surface that predicts the temperature at every location in Madison and surrounding areas.
Interpolate temperature using simple kriging
The Geostatistical Wizard is a guided step-by-step environment for building and validating interpolation models. At each step in the model-building process, you will make important choices that will affect the final temperature map. You can learn more about the Geostatistical Wizard in Get started with Geostatistical Analyst in ArcGIS Pro in the documentation.
- If necessary, open your project.
- On the ribbon, click the Analysis tab. In the Workflows group, click Geostatistical Wizard.

The Geostatistical Wizard appears and shows the available interpolation methods in the left pane and dataset options in the right pane.
- Under Geostatistical methods, choose Kriging / CoKriging.

The right side of the Geostatistical Wizard updates to show applicable Kriging/CoKriging options.
- Under Input Dataset 1, set the following parameters:
- For Source Dataset, choose Temperature_Aug_08_8pm.
- For Data Field, choose TemperatureF.

By choosing Temperature_Aug_08_8pm as the source dataset and TemperatureF as the data field, you specify that you want to perform simple kriging on the temperature measurements. By not providing a second dataset, you'll perform kriging rather than cokriging. You can learn more about cokriging in Understanding cokriging in the documentation.
- Click Next.
On the second page of the Geostatistical Wizard, you'll specify which type of kriging you want to perform and configure options applicable to that type of kriging.
- In the left pane, under Simple Kriging, confirm that Prediction is selected.

Note:
Simple kriging is one of the oldest and most-studied kriging models, and it will serve as a robust baseline for temperature interpolation. Choosing the Prediction option specifies that you want to predict the value of the temperature. Other options allow different types of outputs. You can learn more about the other output options in What output surface types can the interpolation models generate? in the documentation.
- For Dataset #1, change Transformation type to None.
This parameter specifies that you won't perform any transformations.

- Click Next.
The Semivariogram/Covariance Modeling page appears.

- Under General Properties, change Function Type to Semivariogram.
This parameter updates the graph from covariance to semivariogram.

The graph on the left now updates to display a semivariogram instead of covariance. The semivariogram is the mathematical backbone of kriging and fitting a valid semivariogram is almost always the most difficult and time-consuming step in building a kriging model.

Note:
The semivariogram can be considered a quantification of Waldo Tobler's First Law of Geography: "Everything is related to everything else, but near things are more related than distant things."
The semivariogram defines exactly how similar the values of the points are given how far apart they are. The x-axis of the semivariogram is the distance between any two data points, and the y-axis is the expected squared difference between the values of the two points. For any two locations on the map, you can use a semivariogram to estimate the similarity in the data values of the two locations. Because near points are more similar than distant points, the semivariogram always increases with distance before eventually becoming flat.
The semivariogram pane is composed of three sections:
- Semivariogram—The graph in the upper left of the pane, containing binned values (red points), averaged values (blue crosses), and the semivariogram model (blue curve).
- General Properties—The parameters in the right pane of the page, used to configure the shape of the blue semivariogram model.
- Semivariogram map—Located on the lower left of the page, used to detect anisotropy. Anisotropy will not be discussed in this tutorial.
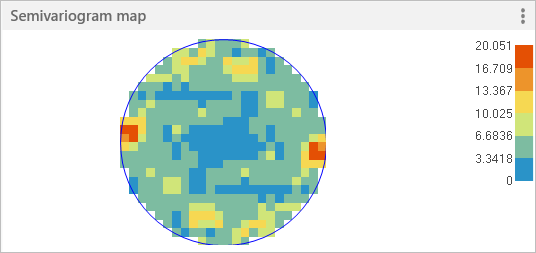
The semivariogram is configured by three parameters that are found in General Properties:

- Nugget—The value of the semivariogram at the y-axis, which represents the expected squared difference in the value of points that are zero distance apart. While in theory the expected squared difference for these points should be zero, a nugget value greater than zero often occurs due to microscale variation and measurement errors.
- Major Range—The distance where the semivariogram becomes flat. If two points are separated by a distance larger than the major range, the points are considered uncorrelated.
- Partial Sill—The value of the semivariogram at the major range is called the sill. The partial sill is calculated by subtracting the nugget from the sill and represents the expected squared difference in value between points that are spatially uncorrelated. This value provides information about the variance of the underlying spatial process.
Note:
The details of the semivariogram parameters do not need to be deeply understood for this tutorial. Learn more at Understanding a semivariogram: The range, sill, and nugget in the documentation.
The goal of the semivariogram page is to configure the parameters in General Properties such that the blue semivariogram passes as closely as possible through the middle of the binned and averaged values in the semivariogram graph.
Note:
The binned (red points) and averaged (blue crosses) values in the semivariogram graph are calculated directly from the input points using sectors that are defined by the Lag Size and Number of Lags parameters in General Properties. These averaged and binned values are together called an empirical semivariogram. The semivariogram model (blue curve) is then fitted to this empirical semivariogram using a simple curve-fitting algorithm. Learn more at Empirical semivariogram and covariance functions in the documentation.
- Change Model #1 to Spherical.

The blue semivariogram slightly changes after changing the model.
Note:
There are many ways to fit a semivariogram to the same binned and averaged points, and every semivariogram model will estimate a different semivariogram for the same binned and averaged points. All semivariogram models will honor the same nugget, range, and sill, but they will have slightly different shapes.
There is a lot of detail packed into the semivariogram page, and it is often difficult even for experienced geostatisticians to determine the appropriate parameters of a semivariogram. For this reason, the Optimize model button was created.
The purpose of the Optimize model button is to automate finding a nugget, major range, and partial sill that result in the smallest root mean square cross-validation error (cross-validation will be shown and explained later in this tutorial). The Geostatistical Wizard does not apply this optimization by default only because it can sometimes take a long time to calculate.
- Under General Properties, click the Optimize model button.

The optimization of the entire model begins. For this small dataset, it completes quickly.
After optimization, the semivariogram and parameters are updated. These are the values that you will use for your first kriging model.
- Click Next.
The wizard updates to display the Searching Neighborhood page, which consists of a preview of the prediction map along with parameters that control the searching neighborhood.

Note:
You can click anywhere in the preview surface and see the predicted value at that location in the Identify Result section on the lower right. Alternatively, you can type an x,y coordinate, and the center of the searching circle will move to the specified location.
Each prediction is based on neighboring input points, and this page allows you to control how many neighbors will be used and which direction the neighbors will come from. Because your temperature measurements are evenly spread over the map, the default searching neighborhood does not need to be altered. If the input points were more clustered or unevenly spaced, you would need to account for this in the searching neighborhood.
- Under Identify Result, change X to 571000 and Y to 290000. Press Enter between each entry.

The center of the searching circle moves to the specified x,y coordinate in the middle of a hot part of the city.
Have you pinpointed the center of a heat island at this location? No. Heat islands don't really have a center—they tend to spread out across a city.

At this x,y location, Identify Result predicts that the temperature is 83.26 degrees with a standard error of 0.51 degrees. Standard errors quantify the uncertainty in the predicted values. The larger the standard error of the prediction, the higher the uncertainty in the predicted value.
Note:
If the predictions are normally distributed, you can construct margins of error for each predicted value based on this rule: Double the standard error and add it to and subtract it from the predicted value to create a 95 percent confidence interval.
- In this location, for example, the lower bound of the 95 percent confidence interval is (83.26 – 2 * 0.51) = 82.24.
- The upper bound of the confidence interval is (83.26 + 2 * 0.51) = 84.28.
Therefore, the best estimate for the temperature at this location is 83.26 degrees Fahrenheit, but you can be 95 percent confident that the true temperature is somewhere between 82.24 and 84.28 degrees Fahrenheit.
- For Identify Result, change X to 572000 and Y to 307000. Press Enter between each entry.

The prediction location moves to the northern part of the study area in the coldest part of the map. The predicted value for this location is about 75.22 degrees with a standard error of 1.76. At this location, the standard error is much larger. This is because there are fewer temperature measurements toward the top of the map than there are in the city center. This results in larger uncertainty in temperature predictions in areas with fewer measurements.
Next, you will explore the cross-validation page. The cross-validation page displays various numerical and graphical diagnostics that allow you to assess how well your interpolation model fits your data. Cross-validation is a leave-one-out validation method that sequentially hides each input point and uses all remaining points to predict back to the location of the hidden point. The measured value at the hidden point is then compared to the prediction value from cross-validation; the difference between these two values is called the cross-validation error.
- Click Next to display the cross-validation page.
Note:
The logic of cross-validation is that if your interpolation model is accurate and reliable, the remaining points should be able to accurately predict the measured value of the hidden point. If the predictions from cross-validation are close to the measured temperature values, this gives you confidence that your model can accurately predict temperature values at new locations.
- Review the Summary panel on the right side of the cross-validation page.
The summary is useful for quickly assessing the overall accuracy and reliability of the model. Each summary statistic provides different information about the model.

Diagnostic Value Significance Count
139
The number of input points.
Mean—The average of the cross-validation errors
0.144
This provides a measure of bias. A biased model is one that tends to predict values that are either too high or too low on average. If the model is unbiased, this value should be close to zero.
Root-Mean-Square—The square root of the mean squared error
1.775
This RMS measures how close the predicted values are to the measured values on average. The smaller the value, the more accurate the predictions.
Mean Standardized—A standardized version of the mean error
0.044
A value close to zero indicates that the model is unbiased. Because this value is standardized, it can be compared between different models that use different data and units.
Root-Mean-Square Standardized—A standardized version of the root mean square
1.075
This value quantifies the reliability of the standard errors of prediction. This value should be close to one. Significant deviation from one indicates that the standard errors of prediction are not accurate. It is standardized, so it can be compared between different models.
Average Standard Error—The average of the standard errors at the input point locations
1.568
This value should be close to the root mean square. If this value significantly deviates from the root mean square, this indicates that the standard errors may not be accurate.
Overall, these statistics are adequate to justify the accuracy of your kriging model.
- The Mean statistic indicates that on average the temperature predictions are 0.14 degrees too high, which is a small amount of bias and should not be concerning.
- The Root-Mean-Square statistic indicates that on average the predictions differed from the measured values by a little less than two degrees.
- Because the Root-Mean-Square Standardized statistic is larger than one, this indicates that the standard errors are being slightly underestimated.
- On the graphical diagnostics pane, click the Predicted tab to select it, if necessary.

The Predicted graph displays a scatterplot of the cross-validation predictions (x) versus measured values (y) for each input point. In addition, a blue regression line is fitted to the data and a gray reference line is used to compare the blue regression line to the ideal. If your interpolation model is valid, the predictions should be approximately equal to the measured values, so the regression line would follow a 45-degree angle.
In your graph, the blue regression line follows the reference line very closely, which gives you further confidence in the accuracy of your model.
- Click the Error tab.

Notice in the Error graph, your blue regression line is decreasing. This indicates that the interpolation model is smoothing the data, meaning that large values are being underpredicted, and smaller values are being overpredicted. Some degree of smoothing occurs in almost every geostatistical model, and in this result, smoothing is not severe.
- Click the Normal QQ Plot tab to display the distribution of standardized errors versus the equivalent quantiles from the standard normal distribution.

In the Normal QQ Plot graph, if the red dots fall close to the gray reference line, it indicates that the predictions follow a normal distribution. In your graph, the red points do generally fall close to the reference line, but there are some deviations, especially for the points on the upper right part of the graph. While interpreting QQ plots is not an exact science, your graph indicates that you are justified in assuming that the predictions follow a normal distribution.
- Click Finish.
The final page of the wizard is the Method Report page, which displays all the parameters and settings that were used for the interpolation.
- On the Method Report page, click OK.
The Geostatistical Wizard closes and a layer named Kriging, showing predicted temperature values, is added to the Contents pane of your map.

Explore the Kriging layer on the map
Previously, you used the Geostatistical Wizard to interpolate the temperature measurements using simple kriging. You created a geostatistical layer of your kriging results. Geostatistical layers are custom layers that are only created and analyzed in the ArcGIS Geostatistical Analyst extension. They allow fast visualization and analysis, and they can be exported to raster or feature formats. Next, you'll explore your geostatistical layer on the map.
- In the Contents pane, uncheck the Temperature_Aug_08_8pm layer.
- Expand the Kriging layer legend to review the symbology used to indicate warmer and cooler interpolated temperatures.
The legend appears.

The urban heat island effect is clear just from looking at the map. The highest predicted temperatures are in the downtown area of Madison, with temperatures generally in the range of 80 to 84 degrees. Lower predicted temperatures are in the surrounding suburban and rural areas, with temperatures in the range of 73 to 78 degrees.
- Click several locations on the map to preview predicted temperatures and the standard error of the prediction. Make sure to click some areas in the middle of the city as well as some locations in the suburban and rural areas outside the city.

As you investigate higher predicted temperature locations in the middle of the city, notice the associated lower standard errors. It is safe to assume that the predicted temperatures are higher due to the urban heat island effect, and the standard errors are lower because there are more temperature measurements in the middle of the city.
- In the Contents pane, for the Kriging layer, collapse the legend and turn the layer off.
- Turn on Temperature_Aug_08_8pm.
- Save the project.
You used the Geostatistical Wizard to create a layer predicting the temperature in Madison, Wisconsin, on August 8, 2016, at 8:00 p.m. You started with 139 points measuring the temperature across the city. You found evidence of the urban heat island effect by exploring the temperature measurements using symbology and the histogram chart. To verify this observation, you used the Geostatistical Wizard to interpolate the temperature measurements using simple kriging. By creating a continuous layer predicting the temperature across Madison and surrounding townships, you confirmed that there is nearly a 10-degree difference in temperature between the middle of the city and surrounding rural areas.
Next, you will interpolate the temperature measurements again using a newer type of kriging called empirical Bayesian kriging. You will then compare the results from empirical Bayesian kriging to the results from simple kriging.
Interpolate temperature using empirical Bayesian kriging
Previously, you explored the temperature measurements in Madison, Wisconsin, and used the Geostatistical Wizard to create a simple kriging layer predicting the temperature across the entire city, which confirmed the presence of the urban heat island effect. The simple kriging model that you created is a classical kriging model, and it is the exact kind of model that you would expect to find in geostatistical textbooks and published scientific journals. In recent years, however, the rapid increase in computer processing power has led to the development of more sophisticated kriging models that are both more accurate and easier to configure. In this section, you will interpolate the temperature measurements using one of these new kriging models known as empirical Bayesian kriging.
Empirical Bayesian kriging (EBK) was developed specifically to overcome some of the more difficult theoretical and practical limitations of classical kriging. By far, the biggest limitation of classical kriging is the assumption that one single semivariogram can accurately represent the spatial structure of the data everywhere. Recall that the semivariogram represents the expected difference in data value for pairs of points that are a given distance apart. Regardless of where the points are on the map, if two pairs of points are the same distance apart, they are supposed to have the same difference in data values. However, for most datasets this assumption is not reasonable. One semivariogram model may fit best in one part of the map and a completely different semivariogram model may fit best in a different part of the map. In situations like this, you cannot hope to find a single semivariogram model that accurately represents the data everywhere on the map.
Even if there were a single semivariogram that fit well everywhere in the dataset, you would still need to estimate it. Unfortunately, the mathematical equations behind classical kriging assume that the semivariogram has been modeled perfectly, and any inaccuracy in the semivariogram parameters will not be properly accounted for in the predictions and standard errors. Because the math of kriging is based entirely on this single semivariogram, it is critical to estimate it as well as you possibly can. This is why there are so many parameters that can be used to change the shape of a semivariogram: you need as much flexibility as possible to accommodate all of the possible spatial structures of different datasets.
Empirical Bayesian kriging overcomes these problems through a process of subsetting and simulation. EBK starts by dividing the input data into small subsets. In each subset, a semivariogram is estimated automatically, and this semivariogram is used to simulate new data values in the subset. These simulated data values are then used to estimate a new semivariogram for the subset. This simulation and estimation process repeats many times, and it results in many simulated semivariograms in each subset. These simulations are then mixed together to produce the final prediction map.
By estimating the semivariograms on small subsets, different semivariograms will be estimated in different regions of the study area. This allows the model to change locally, and you no longer need to assume that a single semivariogram model can fit the data everywhere. Additionally, by simulating many semivariograms in each subset, you do not have to worry as much about the accuracy of any single semivariogram. When all math is based on a single semivariogram, you must be very careful to make sure that it is as good as it possibly can be, but when many semivariograms are simulated, it is not critical that each of them be perfect.
Perform empirical Bayesian kriging in the Geostatistical Wizard
You will use the Geostatistical Wizard to interpolate the temperature measurements using empirical Bayesian kriging.
Note:
Due to the computational cost of the simulations in EBK, many mathematical operations are optimized for different processors. Depending on the hardware of your computer, you may get slightly different results in this section. These differences can be as large as 1 percent in some cases.
- If necessary, open your project.
- On the ribbon, on the Analysis tab, in the Workflows group, click Geostatistical Wizard.
- For Geostatistical methods, choose Empirical Bayesian Kriging.

- Under Input Dataset, for Source Dataset, choose Temperature_Aug_08_8pm. For Data Field, choose TemperatureF.

- Click Next to update the Empirical Bayesian Kriging semivariogram and preview.
The top left pane displays a preview of the interpolated surface with a searching circle centered in the middle of the data extent.

The lower right displays Identify Result.

General Properties shows parameters for the semivariograms and the searching neighborhood.

Parameters in General Properties provide control over subsets and simulations in EBK:
- Subset Size specifies the number of points in each subset.
- Overlap Factor allows you to control how much these subsets overlap each other.
- Number of Simulations controls how many semivariograms will be simulated in each subset.
The Simulated semivariograms (blue lines) and Empirical semivariogram (blue crosses) are displayed in the lower left. The median semivariogram is solid red, and the first and third quartiles are displayed as dashed red lines.

- Under General Properties, for Subset Size, type 50 and press Enter.

The preview surface updates to reflect the new subset size. With 139 input points, using a subset size of 50 will create approximately three subsets. This ensures that the semivariograms will be sufficiently estimated at a local level, while still maintaining enough points in each subset to reliably estimate the semivariogram parameters.
- Under Identify Result, change X to 571000 and Y to 290000. Press Enter between each entry.

The predicted temperature at this location is about 83.39 degrees with a standard error of 0.61 degrees. In the previous section, simple kriging predicted 83.26 degrees with a standard error of 0.51 degrees at this same location.
Note:
Both simple kriging and EBK predict nearly the same temperature, but there is a notable difference in the standard errors of the predictions. This is because simple kriging almost always underestimates standard errors due to only using a single semivariogram. While a larger standard error in EBK seems to imply that EBK has larger uncertainty than simple kriging, the truth is that the standard errors of simple kriging are incorrectly low.
At this location (571000, 290000), the semivariograms seem to pass through the averaged values (blue crosses) fairly well, particularly at short distances. The averaged values at the largest distances tend to be on the lower end of the spectrum, but it is most critical to properly model the semivariogram at short distances, as these are the distances that will contribute most to the predicted values.

- In Identify Result, change X to 572000 and Y to 307000. Press Enter between each entry.
The prediction location moves to the northern part of the study area in the coldest part of the map. The predicted value for this location (572000, 307000) is about 74.15 degrees with a standard error of 2.29. Simple kriging predicted about 75.22 degrees with a standard error of 1.76. This time, the two predictions differ by a full degree, but this is likely due to the larger uncertainty in the predicted values at this location. This uncertainty can be seen in the larger standard errors, different than the previous x,y location.

- Click other locations on the preview surface to see the predicted values and the simulated semivariograms until you are satisfied that the semivariograms seem to fit the averaged values well almost everywhere on the map.
- Click Next to display the cross-validation page.
As with simple kriging, the cross-validation page displays summary statistics on the right and graphical diagnostics on the left. In the EBK summary statistics, there are now three additional statistics that did not appear in simple kriging:
- Average CRPS—This statistic simultaneously quantifies the accuracy and stability of the model, and it should be as small as possible. Unfortunately, it has no direct interpretation, and it can only be used to compare different interpolation models.
- Inside 90 Percent Interval—The percent of cross-validation points contained in a 90 percent prediction interval. This value should be close to 90. Your value of 89.928 is nearly perfect.
- Inside 95 Percent Interval—The percent of cross-validation points contained in a 95 percent prediction interval. This value should be close to 95. Your value of 96.403 is quite close to the ideal value of 95.
The following table shows a comparison of cross-validation summary statistics from EBK and simple kriging:
Note:
Your values may differ slightly from the table below due to rounding.
Summary statistic Simple kriging EBK Mean
0.144
0.158
Root-Mean-Square
1.775
1.715
Mean Standardized
0.044
0.049
Root-Mean-Square Standardized
1.075
0.995
Average Standard Error
1.568
1.683
- Larger Mean and Mean Standardized values in EBK indicate that it has slightly more bias than simple kriging, but overall both models have very small amounts of bias.
- The slightly lower Root-Mean-Square value indicates that on average EBK predicts slightly more accurate temperature values.
The biggest difference in the two models is that the standard errors in EBK are much more accurate.
- The larger Average Standard Error value in EBK shows that on average, EBK is estimating larger standard errors than simple kriging.
- The nearly perfect Root-Mean-Square Standardized value in EBK (recall that ideally it should be one) indicates that these standard errors are being more correctly estimated.
- The Average Standard Error value of EBK also more closely matches that Root-Mean-Square value than it does in simple kriging.
Taken together, this is strong evidence that the EBK model is more reliable than the simple kriging model.
- Confirm that the graphical diagnostics pane is displaying the Predicted graph.

The graph shows predicted values from cross-validation versus measured values. The blue regression line is so close to the gray reference line that you can hardly see the reference line. In simple kriging, the regression line was not as perfectly aligned with the reference line. This should give you further confidence that the EBK model is more reliable.
- Click the Error tab.

Like the simple kriging model before, the blue regression line is slightly decreasing, which indicates that the model has performed smoothing of the data, but this smoothing is not severe.
- Click the Normal QQ Plot tab.

The red points very closely follow the gray reference line. There is still some deviation from the reference line for the largest values, but this deviation is smaller than it was in simple kriging. Based on this graph, you can safely assume that the predictions follow a normal distribution.
- Click Finish.
- On the Method Report page, click OK.
The Geostatistical Wizard closes, and the Empirical Bayesian Kriging geostatistical layer is added to the Contents pane. This layer has the same symbology as the Kriging layer, so they can be visually compared.

- In the Contents pane, turn off Temperature_Aug_08_8pm.
- Turn on Kriging and ensure the Empirical Bayesian Kriging layer is on. Click Empirical Bayesian Kriging to select it.
- On the ribbon, on the Geostatistical Layer tab, in the Compare group, click Swipe.

- On the map, swipe up and down or left and right to display the difference between the Empirical Bayesian Kriging and Kriging layers.

- On the Map tab, in the Navigate group, click Explore to deactivate the Swipe tool.
Note:
You can also deactivate the Swipe tool by right-clicking and choosing Exit Swipe Mode.
- In the Contents pane, turn off the Empirical Bayesian Kriging and Kriging layers.
- Save the project.
You have interpolated the temperature measurements using Empirical Bayesian kriging in the Geostatistical Wizard. As with simple kriging in the previous section, you could confirm the presence of an urban heat island on the prediction map; the center of the city is notably warmer than the surrounding areas. Using cross-validation, you showed that EBK produced a moderately more accurate temperature prediction map, particularly for the standard errors of predicted temperatures.
Next, you will use an even more sophisticated version of kriging called EBK Regression Prediction, which will allow you to incorporate the locations of impervious surfaces into the interpolation.
Incorporate explanatory variables with EBK Regression Prediction
Previously, you learned how to use the Geostatistical Wizard to interpolate temperature measurements in Madison, Wisconsin, on August 8, 2016, at 8:00 p.m. You first used a classical interpolation method called simple kriging. You then learned to use a more modern and robust method called empirical Bayesian kriging (EBK) that provided moderately more accurate predictions using fewer parameters and settings. In this module, you will learn how to incorporate explanatory variables into the interpolation using EBK Regression Prediction.
An explanatory variable (sometimes called a covariate) is any dataset that is related to the variable you are investigating and can be incorporated into a model to improve its accuracy or reliability. As the name implies, EBK Regression Prediction is a regression-kriging method that is a hybrid of EBK and linear regression. EBK Regression Prediction allows you to use explanatory variable rasters that you know are related to the variable you are interpolating.
For these temperature measurements, you will incorporate the locations of impervious surfaces into the interpolation. Impervious surfaces are important contributors to urban heat islands because these surfaces (usually buildings and other manmade structures) trap the heat in the middle of dense cities and prevent it from diffusing into surrounding rural areas.
A deep understanding of regression is not required to complete this section, but a little background will be helpful. Both kriging and regression make predictions by explicitly separating an estimate of the average value and an estimate of the error:
Prediction = Average + ErrorIn regression, the average component of the prediction is estimated with a weighted sum of explanatory variables, and the error component is assumed to be random noise. In this sense, all of the predictive power in regression comes from the average component, and the error component is just noise that you want to minimize.
In kriging, however, the predictive power comes from the error component, and the average is equal to the average of the measured values of all the input points (or some other specified constant). The error component is estimated by the semivariogram and the values of the neighboring points. If the values of the neighbors tend to be above the average value of all input points, the error component will be positive, and the prediction will be larger than the average value of all the points. Conversely, if the values of the neighbors are below the average, the error component will be negative, and the prediction will be lower than the average.
At their mathematical cores, regression operates only on the average component and kriging operates only on the error component. Regression-kriging, however, operates on both components at the same time. It simultaneously estimates the average using linear regression and the error component using EBK. Because both kriging and regression are special cases of regression-kriging, EBK Regression Prediction has higher predictive power than either kriging or regression individually.
Note:
Due to the computational cost of the simulations in EBK and EBK Regression Prediction, many mathematical operations are optimized for different processors. Depending on the hardware of your computer, you may get slightly different results in this section. These differences can be as large as 1 percent in some cases.
Incorporate an Impervious Surface layer from the Living Atlas
In this section, you will add a raster layer from the ArcGIS Living Atlas of the World and extract the Impervious Surface values within your study area. This layer comes from the National Land Cover Database (NLCD) and the value of each cell represents the proportion of the cell that is impervious to water as a result of development.
- If necessary, open your project.
- On the ribbon, on the Map tab, in the Layer group, click Add Data.
The Add Data window appears.
- In the Add Data window, under Portal, click Living Atlas.

- In the search bar, type Impervious and press Enter.
- In the search results, locate and click USA NLCD Impervious Surface Time Series.

- Click OK to add the layer to your map.
Note:
It may take a few minutes for the layer to load.
![Impervious Surface map] Impervious Surface map]](GUID-509DD17E-1A85-482F-9C54-20D1A1B40BF5-web.png)
The USA NLCD Impervious Surface Time Series layer covers the entire continental United States, but your study area covers the extent of the Madison, Wisconsin, area. As a result, you'll create a subset of the source data to match the extent of your study area by using the Extract By Mask geoprocessing tool.
- On the ribbon, on the Analysis tab, in the Geoprocessing group, click Tools.

The Geoprocessing pane appears.
- In the Geoprocessing pane search box, type extract by mask.
- In the search results, click Extract by Mask.

- In the Extract by Mask tool, set the following parameters:
- For Input raster, choose USA NLCD Impervious Surface Time Series.
- For Input raster or feature mask data, choose Block_Groups.
- For Output raster, type Impervious_Surfaces.
The output raster will be saved in the default geodatabase of the project.

In addition to extracting Impervious_Surface values within your study area, you also want to update the coordinate system to the same projection as the rest of your data and additionally resample the source data to a more suitable cell size of 100 meters. These changes will allow faster calculations later in the tutorial.
- In the Geoprocessing pane, click the Environments tab and change the following parameters:
- For Output Coordinate System, choose Block_Groups.
- For Cell Size, type 100.
- For Extent, click Extent of a Layer, and choose Block_Groups.
The output coordinate system for the output is now set the same as the Block_Groups layer, which is NAD_1983_2011_Wisconsin_TM, and the output cell size is set to resample to 100 meters. The Processing Extent is defined by the Block_Groups layer and sets the X and Y extent values and coordinate system.

- Click Run.
The layer Impervious_Surfaces is added to the map and Contents pane. You will adjust the symbology.
- In the Contents pane, right-click Impervious_Surfaces and choose Symbology.
- In the Symbology pane, for Color scheme, click the drop-down menu, check Show Names, and choose Yellow-Orange-Red (5 classes).

The Impervious_Surfaces layer redraws with the new color scheme. It is a subset of the USA NLCD Impervious Surface Time Series layer and contains extracted values covering the extent of the Block_Groups layer that are resampled to 100-meter cell size in the correct projection needed for your analysis.
You no longer need the USA NLCD Impervious Surface Time Series layer so you'll remove it.
- In the Contents pane, right-click USA NLCD Impervious Surface Time Series and choose Remove.
The USA NLCD Impervious Surface Time Series layer is removed from the map.

- Zoom to the city center.
The highest percentage of impervious surfaces are in the middle of the city and along transportation corridors, and fewer impervious surfaces are located in suburban and rural areas surrounding the city, which generally have higher percentages of vegetation and open space.

There are no impervious surface values covering the lakes. As a result, EBK Regression Prediction will not make temperature predictions across lakes. This is desirable because all your source temperature measurements were taken on the land and are thus unlikely to reliably predict temperature over the lakes. Temperature variation across water is driven by different factors than land temperatures.
Create a scatter plot of temperature and impervious surfaces
You have strong reason to believe that impervious surfaces are related to and contribute to urban heat, but you need to quantify this assumption. To visualize the relationship, you'll extract the values of the Impervious_Surfaces layer and add these values to the temperature layer, and then visualize the relationship using a scatter plot.
- In the Geoprocessing pane, click Back twice to get back to the search box.

- In the search box, type extract multi values. In the search results, click Extract Multi Values to Points.
- In the Extract Multi Values to Points tool, set the following parameters:
- For Input point features, choose Temperature_Aug_08_8pm.
- For Input raster, choose Impervious_Surfaces.
- For Output field name, type Raster_Value.

- Click Run.
- On the Contents pane, right-click Temperature_Aug_08_8pm and click Attribute Table.
The Raster_Value field is added to the Temperature_Aug_08_8pm table. This Raster_Value attribute represents the impervious surface value extracted from the Impervious_Surfaces raster layer for each point location. The value is the percent impervious surface, meaning that percentage of the cell was composed of impervious surfaces. The Raster_Value values range from 0 to 97. Two points have null values.
Next, you'll make a chart to see how the impervious percentage relates to temperature.
- In the Contents pane, right-click Temperature_Aug_08_8pm, point to Create Chart, and choose Scatter Plot.
- If necessary, click the Properties button in the chart area to open the Chart Properties pane.
- In the Chart Properties pane, set the following parameters:
- For X-axis number, choose TemperatureF.
- For Y-axis number, choose Raster_Value.
The chart updates to display the scatter plot titled Relationship between TemperatureF and Raster_Value.

Note:
Your scatter plot may look slightly different if you used a more recent version of the USA NLCD Impervious Surface Time Series layer.
The scatter plot shows a clear positive relationship between the measured temperature (TemperatureF) and the percentage of impervious surfaces (Raster_Value). In addition, the relationship appears to be roughly linear, as the trend line appears to pass through the middle of the points. The higher the percentage of impervious surfaces, the higher the temperature. This linear relationship between the variables is important because linear regression rests on this assumption.
- When you are done exploring the relationship between TemperatureF and Raster_Value scatter plot, close the attribute table, chart, and Chart Properties panes.
- Turn off the Impervious_Surfaces layer.
Interpolate temperature using the EBK Regression Prediction tool
In the previous section, you verified that impervious surfaces are an important explanatory variable for predicting temperature in Madison, Wisconsin. In this section, you will use the EBK Regression Prediction geoprocessing tool to interpolate the temperature measurements using the impervious surfaces as an explanatory variable. You'll then compare the cross-validation results from the EBK Regression Prediction tool to the previous two kriging models and apply meaningful symbology to your results.
Note:
EBK Regression Prediction can be executed from both the Geostatistical Wizard and a geoprocessing tool. The primary advantage of using a geoprocessing tool is the ability to incorporate the tool in a model or script for automation and documentation of a workflow. The Geostatistical Wizard is an excellent way to explore data and test various interpolation techniques and parameters before committing to one specific choice.
- In the Geoprocessing pane, click the Back button. In the search box, type EBK.
- In the search results, click EBK Regression Prediction.
- In the EBK Regression Prediction tool, set the following parameters:
- For Input dependent variable features, choose Temperature_Aug_08_8pm.
- For Dependent variable field, choose TemperatureF.
- For Input explanatory variable rasters, choose Impervious_Surfaces.
- For Output prediction raster, type Temperature_Prediction.

- Expand Additional Model Parameters. For Maximum number of points in each local model, type 50.

This parameter specifies that each subset will have 50 points, which matches the values used in EBK in the previous section.
- Click the Environments tab. For Extent, click Extent of a Layer and choose Block_Groups.
- Click Run.
Note:
It may take several minutes for the tool to execute.
When the geoprocessing is complete, two layers, named EBKRegressionPrediction1 and Temperature_Prediction, are added to the Contents pane. The EBK Regression Prediction tool shows a warning.
The warning indicates two features were not used in the analysis; these two points are very close to the shoreline and have Raster_Value set to null. This warning can be ignored.
- In the Contents pane, turn off Temperature_Prediction.
The only layer visible is EBKRegressionPrediction1.

The EBKRegressionPrediction1 layer shows the same interpolation pattern of urban heat as both simple kriging and EBK, but it clearly has a lot more precision. The contours are more refined, and the temperature values change over much shorter distances, indicating a higher degree of accuracy. No interpolation has occurred over the lakes, and as a result, we see a more realistic temperature map, which once again needs quantitative verification using cross-validation.
- In the Contents pane, right-click EBKRegressionPrediction1 and choose Cross Validation to display a cross-validation window.

The Cross validation window is identical to the final page of the Geostatistical Wizard and allows the exploration of the geostatistical layers results. Summary statistics are organized on the right and graphical diagnostics on the left.

The following table compares summary statistics for this EBK Regression Prediction as well as for the EBK and simple kriging you completed in previous sections:
Note:
You may notice slight variations due to rounding.
Summary statistic Simple kriging EBK EBK Regression Prediction Average CRPS
N/A
0.894
0.784
Inside 90 Percent Interval
N/A
89.928
93.431
Inside 95 Percent Interval
N/A
96.403
94.891
Mean
0.144
0.158
0.104
Root-Mean-Square
1.775
1.715
1.451
Mean Standardized
0.044
0.048
0.042
Root-Mean-Square Standardized
1.075
0.994
0.947
Average Standard Error
1.568
1.684
1.516
- For EBK Regression Prediction, the Average CRPS value is about 20 percent lower than EBK, and the Root-Mean-Square value is about 25 percent lower than EBK. These are both strong indications that EBK Regression Prediction is more accurate than EBK or simple kriging.
- The smaller Mean and Mean Standardized values also show that EBK Regression Prediction has the lowest level of bias, and the Average Standard Error value is closely aligned with the Root-Mean-Square value.
- There is some evidence that the standard errors are being slightly overestimated because the Root-Mean-Square Standardized value is less than one, and the Inside 90 Percent Prediction Intervals and Inside 95 Percent Prediction Intervals contain a slightly different percentage of points than they are expected to (93.431 and 94.891 percent, respectively), but the standard errors look accurate overall.
Based on these statistics, EBK Regression Prediction is clearly the most accurate and reliable of the three kriging models.
- Confirm that the Predicted tab is active in the graphical diagnostics pane.

In the Predicted graph, the regression line (blue) is almost perfectly aligned with the reference line (gray). There is a lot of variability in the points around the regression line, but this graph should give you further confidence in the accuracy of the model.
- Click the Error tab.

Like the two models before, the regression line in the Error graph is trending down. This indicates some smoothing in the model, but once again, the smoothing is not severe.
- Click the Normal QQ Plot tab.

Points in the Normal QQ Plot graph fall closer to the reference line than in either of the previous two models. Even the largest values fall very close to the line. There is some minor deviation from the line for the smallest values, but you can safely assume that the predictions follow a normal distribution based on this graph.
Based on the numerical and graphical cross-validation diagnostics, you now have strong evidence that the EBK Regression Prediction model provides the most accurate predictions of the three models you have used. This is the model that will serve as your recommended procedure for interpolating temperature in Madison, Wisconsin.
Now that you have decided on using the EBK Regression Prediction model, you will apply attractive and meaningful symbology to the Temperature_Prediction raster.
- Close the Cross validation window.
- In the Contents pane, turn off EBKRegressionPrediction1. Turn on Temperature_Prediction.
You will now apply more meaningful symbology to Temperature_Prediction by importing a custom stretch renderer from an existing layer file.
- In the Contents pane, right-click Temperature_Prediction and choose Symbology.
- In the Symbology pane, click the Menu button and choose Import from layer file.

- On the Import Symbology dialog box, browse to the location where you extracted the downloaded project in the first module, double-click the analyze-urban-heat-using-kriging folder, and choose EBKRP_Symbology.lyrx.
The Temperature_Prediction layer symbology updates.

The EBKRP_Symbology.lyrx file contains predefined symbolization methods and properties suitable for the Temperature_Prediction layer.
- Close the Symbology pane.
The layer is symbolized with a stretched color scheme ranging from 73 degrees Fahrenheit in the lightest shade of yellow to 86 degrees in the darkest shade of red. This color ramp matches the one that was used for temperature measurement points in the Temperature_Aug_08_8pm layer.
The urban heat effect is obvious just by viewing the layer. The hottest temperatures are in the middle of the city, and the coldest temperatures are in the surrounding rural areas. However, by including the impervious surfaces layer, you are getting far greater detail in the predicted surface. In some areas, you can even pick out urban corridors and view how the heat flows between the buildings and along the highways and freeways.
- Pan and zoom around the map to investigate any areas that interest you. Click several locations within the city center and suburban and rural areas to identify predicted temperature.
Estimate the average temperature within each block group
Next, you will predict the average temperature within each of the block groups using zonal statistics. Once you predict the average temperature within each of the block groups, you will join the predictions to the block groups and apply relevant symbology to visualize average temperatures.
- In the Contents pane, turn off Temperature_Prediction. Turn on Block_Groups.
- In the Geoprocessing pane, click the Back button, and search for zonal statistics. In the search results, click Zonal Statistics as Table (Spatial Analyst).
- In the Zonal Statistics as Table tool, set the following parameters:
- For Input raster or feature zone data, choose Block_Groups.
- For Zone field, choose OBJECTID.
- For Input value raster, choose Temperature_Prediction.
- For Output table, type Mean_Temperature.
- For Statistics type, choose Mean.

Choosing Mean for the statistics type indicates that you want to determine the average of all temperature predictions within a block group.
- Click Run.
The table appears in the Contents pane, under the Standalone Tables section. It contains 269 records, one for each of the 269 block groups in the study area. In the table, the OBJECTID field identifies individual block groups and the Mean field contains the average predicted temperature within each block group.
Next, you will join the Mean_Temperature table to the block groups in order to add the Mean field values to each individual block group polygon.
- In the Geoprocessing pane, click the Back button, and search for Add Join. In the search results, click Add Join.
- In the Add Join tool, set the following parameters:
- For Input Table, choose Block_Groups.
- For Input Join Field, choose OBJECTID.
- For Join Table, choose Mean_Temperature.
- For Join Table Field, choose OBJECTID.

- Click Run.
Attribute fields from the Mean_Temperature table are now joined to block groups using the OBJECTID to identify each unique block group.
- In the Contents pane, right-click Block_Groups and choose Attribute Table.
- In the Block_Groups attribute table, scroll to the far right and confirm that the MEAN field has been appended to the table.
This field contains the average predicted temperature for each block group.
- Close the Block_Groups attribute table.
Next, you will symbolize the block groups by the predicted average temperature and apply symbology from an imported layer file.
- In the Geoprocessing pane, click the Back button, type Apply Symbology and press Enter.
- In the list of results, click Apply Symbology from Layer tool and set the following parameters:
- For Input Layer, choose Block_Groups.
- For Symbology Layer, browse to the location where you extracted the downloaded project and choose BG_temperature.lyrx.
- Under Symbology Fields, for Type, verify that the value is Value field.
- For Source Field, verify that the value is Mean_Temperature.MEAN.
- For Target Field, verify that the value is MEAN.

- Click Run.
The block group symbology updates to show each block group polygon shaded by the average predicted temperature within that block group. The color range used is the same as the original Temperature_Aug_08_8pm layer. The average temperature follows the same patterns as the prediction raster: the hottest block groups are located in and around the center of the city, and the coldest block groups are in the surrounding suburban and rural areas.
- Open the pop-ups for several block groups that show high mean temperatures.

- Close the pop-up window when you are finished reviewing.
Identify block groups with high numbers of vulnerable residents
You used zonal statistics to predict the average temperature within each of the block groups. Next, you will use a query to identify any block groups that have both high average temperatures and a high density of residents over the age of 65. Elderly residents over 65 are most susceptible to heat-related illnesses, so priority for remedial measures should be given to areas of Madison that have the highest numbers of these at-risk residents. You will build a query expression to select all block groups where the mean temperature is greater than 81 and the density of residents 65 years of age or older is greater than 100,000.
- In the Geoprocessing pane, search for Select Layer.
- In the search results, click Select Layer by Attribute.
Query expressions use the following syntax:
Field name + Operator + Value or Field - In the Select Layer by Attribute tool, set the following parameters:
- For Input Rows, choose Block_Groups.
- For Selection type, choose New selection.
- Under Expression, create the expression MEAN is greater than 81.
Tip:
You may need to remove values after the decimal.

- Click Add Clause to add a second clause to your query.
Expressions can include additional clauses or conditions that are connected to the original clause using a connector such as And or Or. Connectors indicate whether one or both clauses need to be true to select a feature.
- Create the expression And DensityOver65 is greater than 100000.

- Click the Verify button.

This expression selects block groups with an average temperature above 81 degrees Fahrenheit and a density of residents over the age of 65 that is greater than 100,000 people per square kilometer.
- Click Run.
The block groups that match the expressions are selected on the map.

- Close the Geoprocessing pane.
Several block groups are selected based on your criteria. They are all located in downtown areas and areas along transportation corridors, and they represent the areas of the city where there is high potential for heat-related illnesses in the vulnerable population. In an emergency, these are the areas that should be prioritized by health care authorities.
Note:
You may have different block groups selected if you used a more recent version of the impervious surface temperature layer in the previous sections.
As a final check, you will create a scatter plot of the average temperature versus the density of elderly residents to visualize the overall relationship.
- In the Contents pane, right-click Block_Groups, point to Create Chart, and choose Scatter Plot.
- In Chart Properties pane, for X-axis number, choose MEAN.
- For Y-axis number, choose DensityOver65.

The scatter plot updates to show the relationship between average temperature and density of elderly residents. The selected block groups remain selected in the scatter plot and indicate occurrences where the average temperature is above 81 degrees Fahrenheit and the density of residents over the age of 65 is above 100,000.
There appears to be no relationship between average temperature and density of elderly residents. The trend line is very flat with a slightly negative slope, and the scatter plot does not show any marked patterns. This is good news, because it means that elderly residents over 65 do not tend to live in the hottest parts of Madison, Wisconsin.
- In the Relationship between MEAN and DensityOver65 chart, click the single point located at the top of the graph.
The selected block group has a high density of elderly residents (over 700,000) and falls in the middle of the temperature range (around 80 degrees Fahrenheit).

Because this block group has such a high density of elderly residents, the temperature of the block group should be closely monitored by the emergency managers of Madison, Wisconsin. Fortunately, on August 8 at 8:00 p.m., this block group did not experience higher temperatures compared to the rest of Madison.
- Save the project.
Share your work
You have completed your analysis of temperature in Madison, Wisconsin, for August 8, 2016, at 8:00 p.m. All you need to do now is to identify an efficient and suitable way to deliver your results to authorities and the public.
ArcGIS offers several ways for you to share your findings, each appropriate for different audiences. The traditional, static approach is to create a layout that can be printed or exported to a PDF or an image file. For a more dispersed audience, you could consider a more dynamic approach and share results online in the form of a web package, web layer, or web map.

For examples and ideas for sharing your results, review these tutorials:
- Get Started with ArcGIS Online walks you through creating a web app.
- Design a layout in ArcGIS Pro shows a detailed, professional layout view, with explanatory text and elements.
- Get Started with ArcGIS StoryMaps describes how to combine a web map with storytelling.
In this tutorial, you learned how to develop a workflow to access interpolation procedures for analyzing urban heat in Madison, Wisconsin. By exploring the temperature measurements on the map and performing interpolation, you verified the presence of a suspected urban heat island in downtown Madison.
To make a temperature map for all of Madison, you first interpolated the data using simple kriging, one of the oldest and most researched geostatistical methods. This resulted in a scientifically and statistically defensible baseline for the interpolation. Once this baseline was established, you improved the results of the interpolation by using empirical Bayesian kriging. By using locally simulated semivariograms, you improved the accuracy and stability of the interpolated temperatures. Using a scatter plot chart, you then determined that the locations of impervious surfaces were highly related to temperature, and you incorporated this information into the interpolation using EBK Regression Prediction. This resulted in a 25 percent reduction in the Root-Mean-Square cross-validation error compared to EBK.
You competed the workflow by querying and locating census block groups in Madison that have the highest average temperature and the highest density of residents over the age of 65, who are at highest risk for heat-related illnesses.
Using selections, you identified block groups with an average temperature above 81 degrees Fahrenheit and a population density of residents over the age of 65 above 100,000 people per square kilometer. A scatter plot chart revealed that the population density of elderly residents does not seem to be correlated with temperature. This was a desirable result because if elderly residents tended to live in the hottest parts of the city, that would pose extra challenges for emergency managers and health care providers when trying to mitigate the effects of extreme heat events.
The urban heat island effect is present in virtually every major city in the world, and the workflow in this tutorial can be used to analyze other cities and other dates. During the development of this tutorial, various potential explanatory rasters were investigated, including elevation, distance to industry, distance to open spaces, population density, and canopy cover. These variables did not significantly improve the interpolation results for Madison, Wisconsin, on August 8, 2016, at 8:00 p.m., but any of these (and many more) could prove useful for interpolating temperature in other urban settings. You are encouraged to attempt to repeat these exercises using temperature data from different cities on different days. You may find that different explanatory variables are useful for different locations and dates, and you should try to find the variables that work best for your data.
You can find more tutorials in the tutorial gallery.

